フラクタル 4 ・ FRACTAL 4
石川源晃著
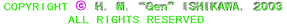
上図は入れ子構造が新しいフラクタル数学の自己相似性を持っていることを説明する図形です。フラクタル
図形の特徴は有限の大きさの図の中に自己相似性の図形を入れ子構造にすることによって、無限の大きさを
折り畳むことができるのです。図は簡単に説明するために一筆書きの二次元図形を使用しましたが、実際の
フラクタル幾何学ではどのような二次元図形であっても、どのような三次元立体構造であっても、自己相似
の構造を持たせることができます。
Above three sets of illustration indicate the nested sets that represent the self contained similarity.
In the FRACTAL geometry, an object having finite scale can hold infinite subject contained inside.
Although the above illustration is simplified in two dimensional drawings, the actual construction
of self-contained similarity will be obtained in three dimensional solid models as well as any kind of
models that are easily found around our human world existed.
上図で矢印の方向に一筆書きで三角形を描きます。中央の図で三角形の一部に同じ形の小三角形を内部に
描きます。その右の図では、さらに小さい三角形を入れ子構造で書きいれて全体の情報を内部に収納する内臓の
自己相似の構造が表現できます。この操作を繰り返せば有限の図形の中に無限の大きさの情報を内蔵させること
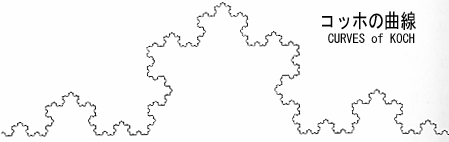
が可能です。この原理はスエーデンの数学者コッホの曲線で、20世紀の前半に既に広く人々に知られていたの
ですが、新しいフラクタル数学はコッホの理論を拡大して複雑な自然現象を表現することが可能になったのです。
上図では、数学的に完全な自己相似の場合を説明しましたが、統計的に自己相似に近い場合、フラクタル数学の
法則が適用できるのです。コンピュータの画像を見て同じように見える場合には、フラクタル関係が成立するのですから、
フラクタル幾何学はコンピュータ時代に適した数学なのです。
Above left view indicates one stroke drawing of a triangle written along the line of an arrow. A small triangle
is written in the center illustration and further smaller triangles are written in the right view. In such
process, the nested sets will demonstrate the self similarity. After the repeated process, one can demonstrate
a sample case that contains almost infinite amount of information in one triangle drawing exhibited. This
kind of example case was described by a Swedish mathematician Helge von Koch (1870-1924) and it is
well known since the early twentieth Century. The theory of Koch is developed further in new FRACTAL
geometry and the self similarity will be justified in another rough case where the statistical analysis proves it.
Thus, we can employ the computer analysis by viewing a similar pattern on the screen to examine the
patterns in self similarity contained.
哲学者はこの世を秩序が保たれた状態と秩序がない無秩序の状態との二つに分けて考えます。新しいカオス
混沌の物理学は秩序状態から無秩序の状態に移行する、
ぎりぎりの極限状態を細かく分析するのです。極限状態では、
フラクタル数学が成立するのです。どのような現象でも、とり扱う数字を並べて、数字の対数分布が
一直線上に並ぶ場合は、その数字はフラクタル分布になることが数学で証明されています。占星学は
実在する天体を組み合わせて予測します。占星学を秩序と無秩序の間の
ぎりぎりの極限状態の現象を研究する
新しいカオス混沌の物理学と、フラクタル数学で解析をすれば、はたしてどのようになるのでしょうか?
Philosophers have been studying our world in two extremities of a good order and a disorder.
New system of CHAOS physics describes the structure in detail at a critical threshold found
in the entrance of a disorder status where in a new FRACTAL geometry is realized. In any
kind of phenomena, the mathematic theory verifies that the FRACTAL distribution of figures
is found in the straight line arrangement of figures; these figures are plotted on the map of
logarithm-logarithm arranged for study. ASTROLOGY has been predicting human affairs by
studying the analysis on the combination formed in the real existing planets in the heaven.
What will be the result of study if we analyze ASTROLOGY with new CHAOS physics and
FRACTAL geometry at the critical threshold of disorder status of our universe encountered?


