フラクタル ２ ・ FRACTAL 2
石川源晃著
なぜ、従来は抽象的にしか表現できなかった複雑な図形を数字で表現できるようになったのでしょうか?
今から約二千年前のギリシャ時代に、人間の身の回りの自然現象が古典物理学で一応は説明されました。
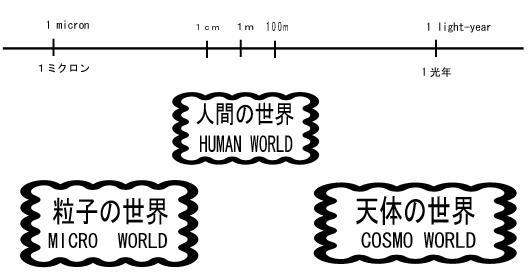
その後の物理学の研究はミクロの世界と天文学の世界に特化されました。そして、人間の身の回りの問題は
医学や心理学の研究対象になりましたが、物理学の研究対象にはなりませんでした。1970年以降の新しい
時代になって、従来は忘れ去られていた人間の身の回りの問題を研究するカオス混沌の物理学が研究される
ようになり、
数学の世界でもフラクラル幾何学のように新しい動きがでてきたのです。ギリシャ時代以来の
数学の考え方では、一次元は線を表現し、二次元は平面を表現し、三次元は立体を表現するというように、
次元というものを整数で表現してきたのですが、この新しいフラクタル数学（フラクタル幾何学・きかがく）
では、海岸線の複雑な線は1.33次元であるというように、分数の数字で表示して、複雑さを表現するのです。
古い時代の哲学や心理学は複雑なものを整理して単純化することで説明をしてきたのです。しかし、自然界
に存在するものは人間が自分勝手に定めた単純化の方法では表現ができないのです。
Why we can come to explain the complicated patters that were not capable to demonstrate by
the science but have been described only in abstract arguments? Orthodox theory of physics
in Grecian age of about two thousand years ago has described the most of phenomena found
around the human life encountered. Since then, researchers were enthusiastic in one of two
separated fields of interest that was either in the MICRO world or the COSMO world specialized.
The phenomena aroused around the human body were studied only by medical schools and
psychological schools found. In and after 1970, we recognize again the human scale of matters
in the study of new CHAOS physics as well as new FRACTAL geometry specialized. In the
orthodox theory of physics and mathematics since Grecian philosophy, one-dimensional figure
describes a line, two-dimensional figure describes a plane and three-dimensional figure describes
a solid, all figures are in integers. In new FRACTAL GEOMETRY, we use decimal figures such as
1.33-dimensions for describing a complicated pattern in sea shore lines. Orthodox theory in
philosophy as well as psychology has been looking things in simplified skeleton as possible by
disregarding complicated structures of phenomena in the natural world encountered. We cannot
describe those matters with our old orthodox theory of human convenience.
次元（じげん）はイタリアの数学者ペアノが1890年に発表したもので百年以上の前のものですが、従来は
平面とか立体とか言う抽象的な表現のものを数字で表現したものです。新しいフラクタル数学はペアノが
整数の数字で一次元、二次元、三次元の言う表現をしたものを小数の数字で表現したのです。前ページの
複雑な図形が一次元と二次元の間の小数で表現できるのは、一次元の単純な線よりも複雑であるけれども、
二次元の平面を覆い隠すほど複雑ではないので1.33次元というのです。
Dimension was described by an Italian mathematician Giuseppe PEANO in 1890 or one hundred
years ago approximately released. He introduced an integral number either in one, or two, or three
for the conventional abstract word of either a line, or a plane, or a solid respectively defined. In new
FRACTAL geometry, we define a complicated natural existence with a decimal number. For instance,
a sea shore line will be more complicated than a straight line of ONE DIMENSION and the sea shore
line will not be enough large as to cover all surface of a plane of TWO DIMENSION. Therefore, this
sea shore line becomes 1.33 DIMENSION in calculation processed.
