People believed long since the old Grecian philosophers a simple smooth change.
Although the ancient people did not recognize other than the simple change, however, the
actual changes that we encounter will change in random way. As we imagine the world after
the outbreak of recent technology new revolution of age, the way of study has been limited in
calm and linear changes mainly because of the budget limitation controlled by the people who
do not recognize the changes. Thus the popular problems including the phase transition either
from the ice to the water or the water to the vapor, are left unsolved yet.
"Does the Flap of a Butterfly’s Wing in Brazil Set Off a Tornado in Texas?”was the question
of EDWARD N. LORENZ of a meteorologist in the United States of America released in 1963.
His question did not cite any reaction in almost ten years. As BENOIT MANDELBROT
born in 1924
in Warsaw, a researcher of the International Business Machines Corporation in the U.S. has
displayed a beautiful pattern designed on the equation given by LORENZ and demonstrated it
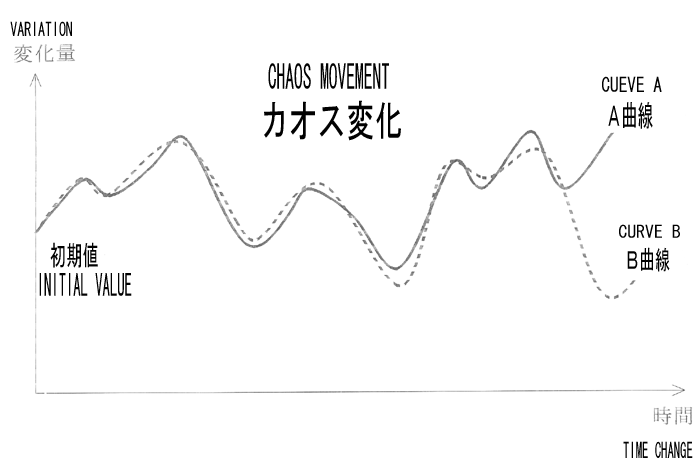
that the study of Lorenz was recognized after 1970s boomed in public. The illustration above
indicates Curve A and Curve B with the same point of Initial Value inaugurated. Two curves
will change simultaneously in the beginning and separate each other suddenly after a short
moment elapsed. Before such moment, the most people are interested in the eventual result
in the movement of curves either in divergent or convergent terminated. But LORENZ did not.
He studied hard on the transiting path in two curves encountered.
自然科学の研究者は早くから矛盾に気がついていましたが研究費を左右する人々
の理解が得られないために研究を放棄してきました。たとえば、氷が水になる途中の変化や、水が蒸気に
変化する途中の状況（位相変化・移相）などの身近な問題の研究が未完成のまま放棄されていました。